선형 회귀란 ?
- 가장 훌륭한 예측선 긋기
예) 성적을 변하게 하는 '정보' 요소를 X라 하고, 이 X값에 의해 변하는 '성적'을 Y라 할 때, X를 독립 변수, Y를 종속 변수라 한다.
-> 선형 회귀란 독립 변수 X를 사용해 종속 변수 Y의 움직임을 예측하고 설명하는 작업
단순 선형 회귀 : 하나의 X값만으로도 Y값을 설명할 수 있을 때
다중 선형 회귀 : 여러개의 X값으로 Y값을 설명할 수 있을 때
최소 제곱법이란?
- 회귀 분석에서 사용되는 표준 방식으로, 실험이나 관찰을 통해 얻은 데이터를 분석하여 미지의 상수를 구할 때 사용되는 공식
- 최소 제곱법 공식을 알고 적용한다면, 일차 함수의 기울기 a와 b(y절편)를 바로 구할 수 있다.
1. a 구하는 공식


2. b 구하는 공식
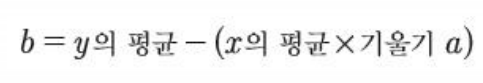

3. 오차의 합 / 평균 제곱 오차(MSE) / 평균 제곱근 오차(RMSE)



p_i는 x_i에 대응하는 '실제 값'
y_i는 x_i가 대입되었을 때 '예측 값'
경사하강법이란?
- 기울기 a를 무한대로 키우면 오차도 무한대로 커지고, a를 무한대로 작게 해도 오차도 무한대로 커진다.(이차 함수 그래프로 표현가능)
- 반복적으로 기울기 a를 변화시켜 m의 값을 찾아내는 방법

1. a_1에서 미분을 구한다
2. 구해진 기울기의 반대 방향 얼마간 이동시킨 a_2에서 미분을 구한다.
3. a_3에서 미분을 구한다
4. "3번"의 값이 0이 아니면 2~3번 과정을 반복한다
학습률

- 기울기의 부호를 바꿔 이동시킬 때 적절한 거리를 찾지 못해 너무 멀리 이동시키면 a값이 한 점으로 모이지 않고 위로 치솟아 버림
- 어느 만큼 이동시킬지를 정해주는 것이 학습률이다.
'기계학습' 카테고리의 다른 글
| [기계학습] 퍼셉트론 / 가중치 / 바이어스 / 가중합(feat. 시그모이드 함수) (0) | 2020.03.29 |
|---|---|
| [기계학습] 규제(데이터 확대, 가중치 감쇠) / 기계학습의 유형 / 그라운드 트루스(Ground truth)란? (0) | 2020.03.29 |
| [기계학습] 과소적합과 과잉적합 / 바이어스와 분산 (0) | 2020.03.26 |
| [기계학습] 기계학습이란 무엇일까? (0) | 2020.03.17 |

